GEOMETRIC
GEOMETRIC (Geometry and Energetics of Ocean Mesoscale Eddies and Their Rectified Impact on Climate) is a project funded by the Natural Environment Research Council to develop and implement an improved representation of ocean eddy-mean flow interaction in ocean climate models. The fundamental idea is to preserve, as far as possible, the symmetries and conservation laws of the underlying Navier-Stokes equations of fluid motion.
GEOMETRIC:
- reproduces the correct dimensional growth rate for the Eady model of baroclinic instability, for which there is an exact mathematical solution;
- models the eddy diffusivity across four orders of magnitude for the nonlinear, fully turbulent Eady problem;
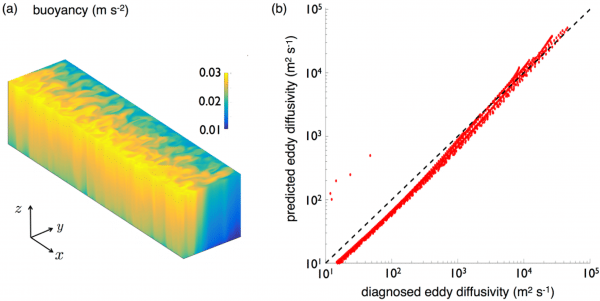
Comparison of diagnosed and predicted eddy diffusivities from fully nonlinear numerical calculations (Bachman et al., 2017). - captures and provides a physical explanation for eddy saturation, the surprising insensitivity of the Antarctic Circumpolar Current to surface wind stress
GEOMETRIC has been implemented in the NEMO ocean model, a key finding from which is that the volume transport of the Antarctic Circumpolar Current, the strength of the Atlantic Meridional Overturning Circulation, and ocean heat content is acutely sensitive to the eddy energy dissipation timescale, a hitherto overlooked parameter in ocean modelling.
Learn more about GEOMETRIC
Read about GEOMETRIC in this poster prepared for the Gordon Research Conference on Ocean Mixing (June 2018).
We have also published a number of papers on GEOMETRIC:
Implementation of GEOMETRIC in NEMO and demonstration of acute sensitivity of global ocean circulation and heat content to eddy energy dissipation timescale:
- Mak, J., D. P. Marshall, G. Madec, and J. R. Maddison, 2022: Acute sensitivity of global ocean circulation and heat content to eddy energy dissipation time-scale. Geophys. Res. Lett., 49, e2021GL097259, doi: 10.1029/2021GL097259.
Implementation of GEOMETRIC in a 3-d ocean circulation model (MITgcm):
- Mak, J., J. R. Maddison, D. P. Marshall and D. R. Munday, 2018: Implementation of a geometrically and energetically constrained mesoscale eddy parameterization in an ocean circulation model. J. Phys.. Oceanogr., 48, 2363-2382, doi:10.1175/JPO-D-18-0017.1.
Initial paper on the GEOMETRIC approach:
- Marshall, D. P., J. R. Maddison and P. S. Berloff, 2012: A framework for parameterizing eddy potential vorticity fluxes. J. Phys. Oceanogr., 42, 539-557, doi:10.1175/JPO-D-11-048.1.
Demonstration that GEOMETRIC leads to skilful eddy diffusivities across several orders of magnitude in the nonlinear Eady spin-down problem:
- Bachman, S. D., D. P. Marshall, J. R. Maddison and J. Mak, 2017: Evaluation of a scalar eddy transport coefficient based on geometric constraints. Ocean Modell., 109, 44–54, doi:10.1016/j.ocemod.2016.12.004.
Theory of eddy saturation and how this is captured by GEOMETRIC:
- Marshall, D. P., D. R. Munday, L. Novak, and M. H. P. Ambaum, 2017: Eddy saturation and frictional control of the Antarctic Circumpolar Current. Geophys. Res. Lett., 44, 286-292, doi:10.1002/2016GL071702.
- Mak, J., D. P. Marshall, J. R. Maddison, S. D. Bachman, 2017: Emergent eddy saturation from an energy constrained eddy parameterisation. Ocean Modell., 112, 125-138, doi:10.1016/j.ocemod.2017.02.007.
Initial attempt to understand how the eddy tilts are set in a barotropic jet usign ray-tracing theory:
- Tamarin, T., J. R. Maddison, J. R., H. Eyal, and D. P. Marshall, 2016: A geometric interpretation of eddy Reynolds stresses in barotropic ocean jets. J. Phys. Oceanogr., 46, 2285-2307, doi:10.1175/JPO-D-15-0139.1.
Rigorous mathematical derivation of the properties of the Eliassen-Palm flux tensor in the thickness-weighted primitive equations, the fundamental object at the heart of GEOMETRIC:
- Maddison, J., and D. P. Marshall, 2013: The Eliassen-Palm flux tensor. J. Fluid Mech., 729, 69-102, doi:10.1017/jfm.2013.259.