The instability of zonal flows to small disturbances underpins our understanding of the scales of motion and their predictability in planetary atmospheres and oceans. Numerous papers have explored aspects of this problem since pioneering work in the late 1940s. The quasi-geostrophic formulation is only valid for small Rossby numbers and large Richardson numbers and requires the stratification of the basic state to be independent of latitude. Formulations with more general validity have until recently been restricted to laterally uniform flows neglecting the Earth’s curvature.

Recently, Bell (2018) has described a simple but novel method for studying stability of any zonal flow that is in thermal wind balance: the linearised primitive equations are reduced to a partial differential equation involving only a single variable, the pressure perturbation; the equation is linear in the pressure perturbation, but nonlinear in the complex phase speed which sets the growth rate of the instability. The method can be used to study the stability of jets on a sphere in which the stratification of the basic state varies with height and latitude, the motions can be non-hydrostatic and the fluid can be compressible. Instabilities associated with different types of critical layers and symmetric and Kelvin Helmholz instabilities can be studied. Integral constraints on the instabilities can also be derived.

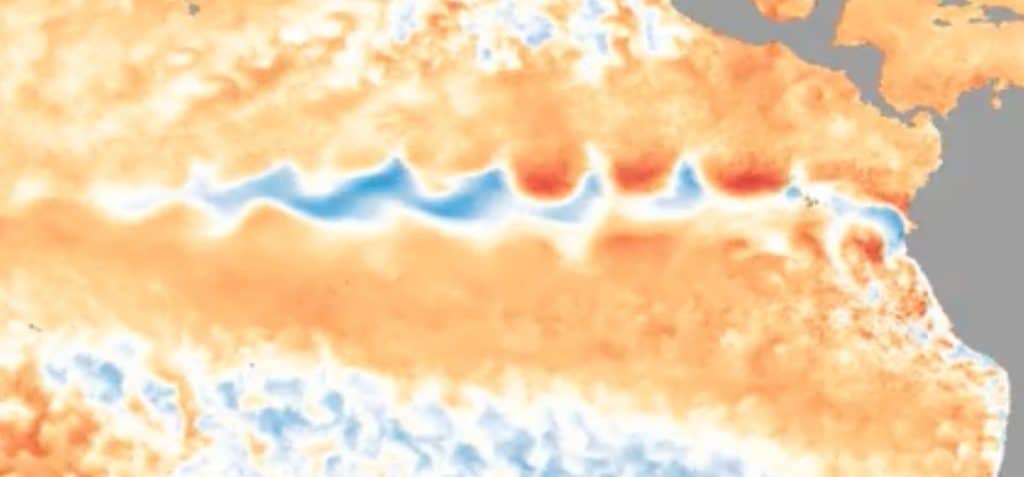
We will investigate the instability of stratified zonal jets near the equator where the Rossby number is large and the Earth’s curvature of fundamental importance. These flows exhibit a number of instabilities that lead, for example, to the formation of tropical instability waves, the heat transport by which is of fundamental importance in setting ocean structure and heat uptake with widespread impact on tropical climate. Understanding the stability properties of these equatorial flows is therefore crucial for understanding the response of tropical climate to anthropogenic forcing.

The dependence of growth rates on the profile of the mean state will be investigated in a hierarchy of progressively more complex zonal flows. The heat and momentum transports by the unstable waves will be calculated and compared with those of tropical instability waves in NEMO ocean model simulations. Three classes of instabilities within the near-surface ocean mixed layer will be studied: symmetric, baroclinic and Langmuir instabilities. The student will diagnose the instabilities in ocean circulation models, explore numerical solutions for a hierarchy of zonal flows, consider theoretical aspects such as integral constraints on the instabilities and neutral modes which mark stability transitions, and calculate the non-linear or weakly nonlinear development of the instabilities. Preliminary investigations of numerical solutions indicate that the growth rates of some instabilities are overestimated unless very fine vertical grid spacing is used: the student will also investigate the vertical resolution that is required for ocean circulation models to avoid misrepresenting the different classes of instabilities.

This project will suit a student with a strong mathematical/physical science background.